Вышла в свет монография профессора СФТИ НИЯУ МИФИ Сергея Петровича Баутина и соавторов «Решение нелинейных уравнений с частными производными тригонометрическими рядами», которая представляет собой значительный шаг вперёд в развитии теории, заложенной более 200 лет назад великим французским математиком Жаном Батистом Жозефом Фурье, предложившим революционный подход к представлению функций в виде бесконечных тригонометрических рядов, что стало основой современной математической физики.
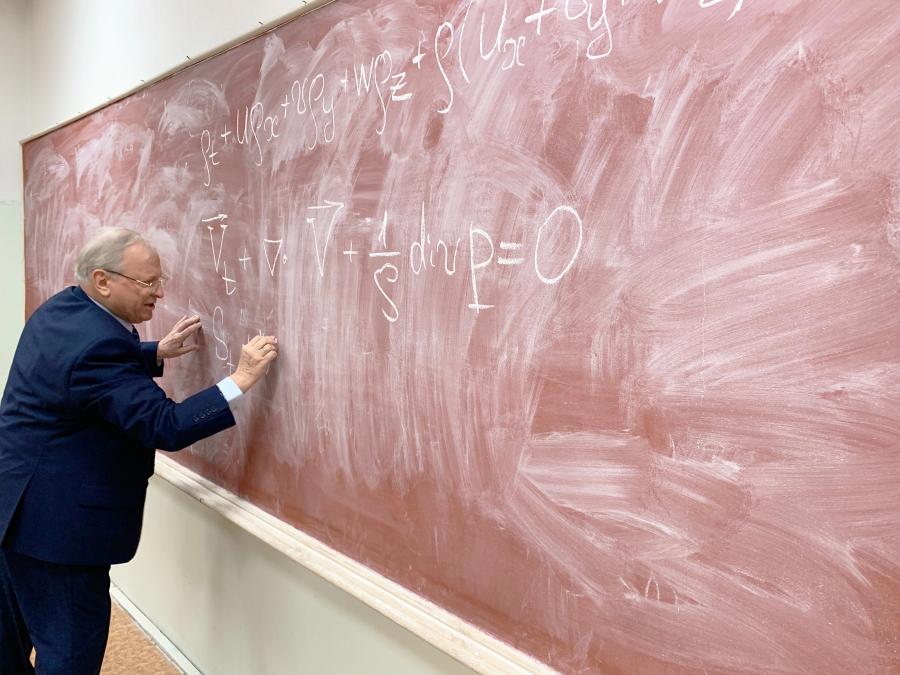
Профессор Сергей Баутин
Профессор Баутин развивает метод Фурье, применяя его к решению сложных нелинейных уравнений с частными производными. «Мы используем тригонометрические ряды, чтобы представить решения нелинейных задач, — объясняет профессор Баутин. — Это развитие идей Фурье, но адаптированное к современным вызовам. Мы доказываем сходимость этих рядов, что позволяет строить приближенные решения с высокой точностью».
Работа профессора Баутина и его коллег из Екатеринбурга, Тюмени и Снежинска имеет не только теоретическое, но и практическое значение. Предложенные в книге методы имеют строгое математическое обоснование и могут быть использованы для тестирования сложных производственных программ, например, в ядерных центрах. «Моя модель может стать инструментом для проверки расчётов, которым раньше не всегда можно было полностью доверять», — подчёркивает профессор.

Баутин С.П., Замыслов В.Е., Карелина О.А., Обухов А.Г. «Решение нелинейных уравнений с частными производными тригонометрическими рядами». — Снежинск: СФТИ НИЯУ МИФИ, 2024.
Монография станет ценным ресурсом для исследователей, инженеров и студентов, изучающих современные методы анализа сложных физических процессов. Работа профессора Баутина и его команды — это пример того, как фундаментальные идеи, заложенные столетия назад, продолжают развиваться и находить новые применения.
Если вы интересуетесь математическим моделированием или работаете в смежных областях, эта книга — must-read. Она не только расширяет границы наших знаний, но и демонстрирует, как теоретическая наука может быть применена для решения реальных практических задач.